qPCR analysis - enhancer zfCRISPRi
Experimental summary
CRISPRi microinjections were performed with Ac/Ds-sgRNAs targeting enhancers versus scrambled. Cells expressing dCas9-SID4x-2a-Citrine under the control of a sox10 (most neural crest, and few non-NC cell types) BAC transgene were FAC-sorted from 24hpf embryos. RNA were isolated for cDNA synthesis by oligo-dT priming. Quantitative real-time PCR (qPCR) was performed using TaqMan Gene Expression Assay on StepOnePlus platform and software v2.3.
TaqMan reagents used:
- Dr03130102_m1 (cdh7a; 66 bp)
- Dr03086868_m1 (pdgfra; 67 bp)
- Dr03436842_m1 (gapdh - endogenous control; 121 bp)
- TaqMan Fast Advanced Master Mix #4444556
Key experimental protocols can be found here.
cdh7a enhancers
Load required packages
library(qpcR)## Loading required package: MASS##
## Attaching package: 'MASS'## The following object is masked from 'package:biomaRt':
##
## select## The following object is masked from 'package:dplyr':
##
## select## Loading required package: minpack.lm## Loading required package: rgl## Loading required package: robustbase## Loading required package: Matrix##
## Attaching package: 'Matrix'## The following objects are masked from 'package:tidyr':
##
## expand, pack, unpacklibrary(tidyverse)
library(ggplot2)
library(RColorBrewer)Load amplification data
Export raw, non-baseline corrected amplification data from qPCR machine e.g. on StepOnePlus software, these would be Rn values (deltaRn is baseline-corrected by StepOnePlus).
Prep dataframe(s) consisting of three columns - Cycle, Run, Rn:
- Cycle = cycle number, in this case from 1 to 40 per Run
- Run = named in the following format Gene*Well_sample_info
- Rn = exported Rn values for each corresponding Cycle/Run
Remove any rows that are not going to be included in the analysis e.g. -RT and water controls (do manually check first they are clean as expected!).
Here, my data is split across four dataframes due to running multiple plates.
data1 <- data.frame(read.table("./data1.txt", header=TRUE, sep="\t"))
data2 <- data.frame(read.table("./data2.txt", header=TRUE, sep="\t"))
data3 <- data.frame(read.table("./data3.txt", header=TRUE, sep="\t"))
data4 <- data.frame(read.table("./data4.txt", header=TRUE, sep="\t"))
head(data1, 10)## Cycles Run Rn
## 1 1 cdh7a*A1_cdh1_1 1.6121
## 2 2 cdh7a*A1_cdh1_1 1.6101
## 3 3 cdh7a*A1_cdh1_1 1.6069
## 4 4 cdh7a*A1_cdh1_1 1.6021
## 5 5 cdh7a*A1_cdh1_1 1.6020
## 6 6 cdh7a*A1_cdh1_1 1.5952
## 7 7 cdh7a*A1_cdh1_1 1.5957
## 8 8 cdh7a*A1_cdh1_1 1.5934
## 9 9 cdh7a*A1_cdh1_1 1.5943
## 10 10 cdh7a*A1_cdh1_1 1.5930Add Group column based on experimental condition.
- cdh = upstream and intronic sgRNAs
- cdhUP = upstream sgRNAs only
- scr = scrambled sgRNAs
data1$Group <- rep(c("cdh","scr"), times=c(240,240))
data2$Group <- rep(c("cdh","scr"), times=c(240,240))
data3$Group <- rep(c("cdh","scr"), times=c(480,480))
data4$Group <- rep(c("cdhUP","scr","cdhUP","scr"), times=c(480,240,480,240))
head(data1, 10)## Cycles Run Rn Group
## 1 1 cdh7a*A1_cdh1_1 1.6121 cdh
## 2 2 cdh7a*A1_cdh1_1 1.6101 cdh
## 3 3 cdh7a*A1_cdh1_1 1.6069 cdh
## 4 4 cdh7a*A1_cdh1_1 1.6021 cdh
## 5 5 cdh7a*A1_cdh1_1 1.6020 cdh
## 6 6 cdh7a*A1_cdh1_1 1.5952 cdh
## 7 7 cdh7a*A1_cdh1_1 1.5957 cdh
## 8 8 cdh7a*A1_cdh1_1 1.5934 cdh
## 9 9 cdh7a*A1_cdh1_1 1.5943 cdh
## 10 10 cdh7a*A1_cdh1_1 1.5930 cdhFinal tidying up. Prefix Group (experimental condition) to existing Run names, check all is in order, then rename columns back to Cycles, Run, Rn.
data1 <- data.frame(data1$Cycles, (paste(data1$Group,data1$Run,sep="^")), data1$Rn)
data2 <- data.frame(data2$Cycles, (paste(data2$Group,data2$Run,sep="^")), data2$Rn)
data3 <- data.frame(data3$Cycles, (paste(data3$Group,data3$Run,sep="^")), data3$Rn)
data4 <- data.frame(data4$Cycles, (paste(data4$Group,data4$Run,sep="^")), data4$Rn)
head(data1, 10)## data1.Cycles X.paste.data1.Group..data1.Run..sep........ data1.Rn
## 1 1 cdh^cdh7a*A1_cdh1_1 1.6121
## 2 2 cdh^cdh7a*A1_cdh1_1 1.6101
## 3 3 cdh^cdh7a*A1_cdh1_1 1.6069
## 4 4 cdh^cdh7a*A1_cdh1_1 1.6021
## 5 5 cdh^cdh7a*A1_cdh1_1 1.6020
## 6 6 cdh^cdh7a*A1_cdh1_1 1.5952
## 7 7 cdh^cdh7a*A1_cdh1_1 1.5957
## 8 8 cdh^cdh7a*A1_cdh1_1 1.5934
## 9 9 cdh^cdh7a*A1_cdh1_1 1.5943
## 10 10 cdh^cdh7a*A1_cdh1_1 1.5930colnames(data1) <- c("Cycles", "Run", "Rn")
colnames(data2) <- c("Cycles", "Run", "Rn")
colnames(data3) <- c("Cycles", "Run", "Rn")
colnames(data4) <- c("Cycles", "Run", "Rn")
head(data1, 10)## Cycles Run Rn
## 1 1 cdh^cdh7a*A1_cdh1_1 1.6121
## 2 2 cdh^cdh7a*A1_cdh1_1 1.6101
## 3 3 cdh^cdh7a*A1_cdh1_1 1.6069
## 4 4 cdh^cdh7a*A1_cdh1_1 1.6021
## 5 5 cdh^cdh7a*A1_cdh1_1 1.6020
## 6 6 cdh^cdh7a*A1_cdh1_1 1.5952
## 7 7 cdh^cdh7a*A1_cdh1_1 1.5957
## 8 8 cdh^cdh7a*A1_cdh1_1 1.5934
## 9 9 cdh^cdh7a*A1_cdh1_1 1.5943
## 10 10 cdh^cdh7a*A1_cdh1_1 1.5930qpcR analysis
We will perform the analysis one experiment at a time (cdh or cdhUP vs scr) using the ratiocalc function. Prep two dataframes containing the appropriate data (dataframe 1 = cdh and scr, dataframe 2 = cdhUP and scr).
data <- data.frame(rbind(data1,data2,data3,data4))
data_cdh <- data[-grep("UP", data$Run), ]
data_cdhUP <- rbind((data[grep("UP", data$Run), ]),(data[grep("scr", data$Run), ]))data_cdh (sgRNAs targeting Group Upstream and Intronic enhancers)
- Set (non) random seed for reproducibility
- Reorganise the data in the exact format required for qpcR package
- Run
pcrbatchfunction to fit sigmoidal model and calculate qPCR efficiency by the ‘window-of-linearity’ method - View if any Runs are tagged
*NAME*/**NAME**due to unsuccessful model fitting/lack of sigmoidal structure
set.seed(584)
data_cdh <- tidyr::spread(data_cdh, Run, Rn)
res_cdh <- pcrbatch(data_cdh, cyc = 1, fluo = NULL,
methods = c("sigfit", "sliwin"),
plot = TRUE,
verbose = FALSE)## Calculating delta of first/second derivative maxima...
## .........10.........20.........30.........40.........50
## .........60
##
## [1] "modlist" "pcrfit"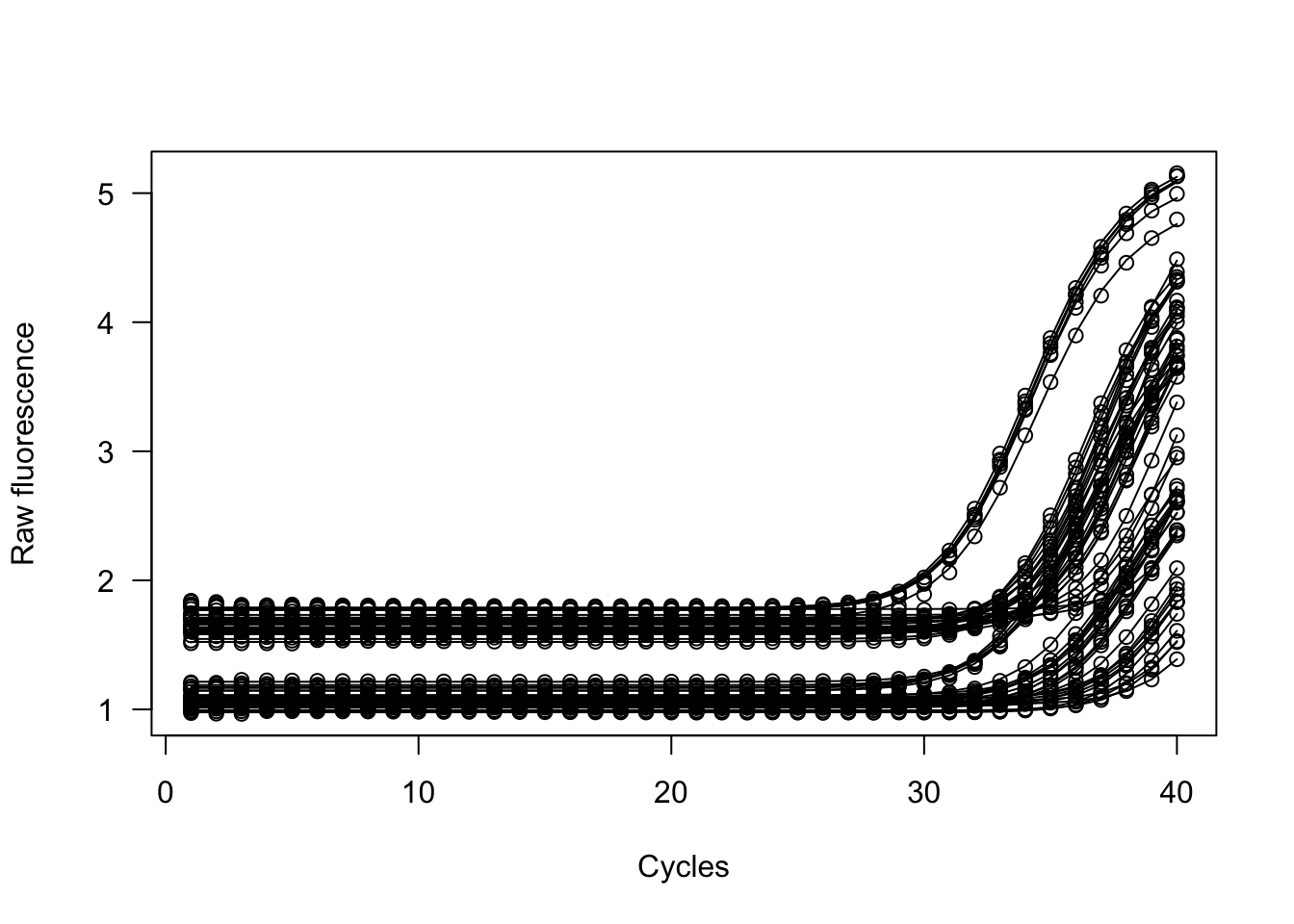
## Analyzing cdh^cdh7a*A1_cdh1_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdh^cdh7a*A1_cdh2_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdh^cdh7a*A2_cdh1_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdh^cdh7a*A2_cdh2_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdh^cdh7a*A3_cdh1_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdh^cdh7a*A3_cdh2_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdh^cdh7a*A4_cdh1_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdh^cdh7a*A4_cdh2_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdh^cdh7a*A5_cdh1_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdh^cdh7a*A5_cdh2_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdh^cdh7a*A6_cdh1_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdh^cdh7a*A6_cdh2_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdh^gapdh*A1_cdh1_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdh^gapdh*A10_cdh2_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdh^gapdh*A11_cdh2_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdh^gapdh*A12_cdh2_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdh^gapdh*A2_cdh1_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdh^gapdh*A3_cdh1_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdh^gapdh*A4_cdh1_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdh^gapdh*A5_cdh1_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdh^gapdh*A6_cdh1_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdh^gapdh*A7_cdh2_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdh^gapdh*A8_cdh2_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdh^gapdh*A9_cdh2_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*A10_scr1_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*A10_scr2_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*A11_scr1_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*A11_scr2_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*A12_scr1_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*A12_scr2_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*A7_scr1_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*A7_scr2_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*A8_scr1_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*A8_scr2_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*A9_scr1_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*A9_scr2_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*B1_scr1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*B2_scr1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*B3_scr1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*B4_scr1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*B5_scr1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*B6_scr1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B1_scr1_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B10_scr2_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B11_scr2_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B12_scr2_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B2_scr1_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B3_scr1_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B4_scr1_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B5_scr1_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B6_scr1_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B7_scr2_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B8_scr2_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B9_scr2_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*D1_scr1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*D2_scr1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*D3_scr1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*D4_scr1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*D5_scr1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*D6_scr1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...colnames(res_cdh)## [1] "Vars" "cdh^cdh7a*A1_cdh1_1" "cdh^cdh7a*A1_cdh2_1"
## [4] "cdh^cdh7a*A2_cdh1_1" "cdh^cdh7a*A2_cdh2_1" "cdh^cdh7a*A3_cdh1_1"
## [7] "cdh^cdh7a*A3_cdh2_1" "cdh^cdh7a*A4_cdh1_2" "cdh^cdh7a*A4_cdh2_2"
## [10] "cdh^cdh7a*A5_cdh1_2" "cdh^cdh7a*A5_cdh2_2" "cdh^cdh7a*A6_cdh1_2"
## [13] "cdh^cdh7a*A6_cdh2_2" "cdh^gapdh*A1_cdh1_1" "cdh^gapdh*A10_cdh2_2"
## [16] "cdh^gapdh*A11_cdh2_2" "cdh^gapdh*A12_cdh2_2" "cdh^gapdh*A2_cdh1_1"
## [19] "cdh^gapdh*A3_cdh1_1" "cdh^gapdh*A4_cdh1_2" "cdh^gapdh*A5_cdh1_2"
## [22] "cdh^gapdh*A6_cdh1_2" "cdh^gapdh*A7_cdh2_1" "cdh^gapdh*A8_cdh2_1"
## [25] "cdh^gapdh*A9_cdh2_1" "scr^cdh7a*A10_scr1_2" "scr^cdh7a*A10_scr2_2"
## [28] "scr^cdh7a*A11_scr1_2" "scr^cdh7a*A11_scr2_2" "scr^cdh7a*A12_scr1_2"
## [31] "scr^cdh7a*A12_scr2_2" "scr^cdh7a*A7_scr1_1" "scr^cdh7a*A7_scr2_1"
## [34] "scr^cdh7a*A8_scr1_1" "scr^cdh7a*A8_scr2_1" "scr^cdh7a*A9_scr1_1"
## [37] "scr^cdh7a*A9_scr2_1" "scr^cdh7a*B1_scr1-1" "scr^cdh7a*B2_scr1-1"
## [40] "scr^cdh7a*B3_scr1-1" "scr^cdh7a*B4_scr1-2" "scr^cdh7a*B5_scr1-2"
## [43] "scr^cdh7a*B6_scr1-2" "scr^gapdh*B1_scr1_1" "scr^gapdh*B10_scr2_2"
## [46] "scr^gapdh*B11_scr2_2" "scr^gapdh*B12_scr2_2" "scr^gapdh*B2_scr1_1"
## [49] "scr^gapdh*B3_scr1_1" "scr^gapdh*B4_scr1_2" "scr^gapdh*B5_scr1_2"
## [52] "scr^gapdh*B6_scr1_2" "scr^gapdh*B7_scr2_1" "scr^gapdh*B8_scr2_1"
## [55] "scr^gapdh*B9_scr2_1" "scr^gapdh*D1_scr1-1" "scr^gapdh*D2_scr1-1"
## [58] "scr^gapdh*D3_scr1-1" "scr^gapdh*D4_scr1-2" "scr^gapdh*D5_scr1-2"
## [61] "scr^gapdh*D6_scr1-2"No runs tagged, so proceed with calculating ratios between experimental conditions.
- We assign each Run into their respective group, in the order shown with
colnames(res_cdh).
- “gs” = gene-of-interest, sample (experimental)
- “rs” = reference gene, sample (experimental)
- “gc” = gene-of-interest, control (scrambled)
- “rc” = reference gene, control (scrambled)
group_cdh <- rep(c("gs","rs","gc","rc"), times=c(12,12,18,18))- Finally, we compute the ratios between the two conditions (treatment/control) - see
ratiocalcdocumentation for more details. We are interested in the Permutation results (not Monte Carlo or Error Propagation) - seepropagatedocumentation for more details.
cdh_ratios <- ratiocalc(res_cdh, group = group_cdh, plot = TRUE,
which.eff = "sli", type.eff="mean.single", which.cp="cpD2")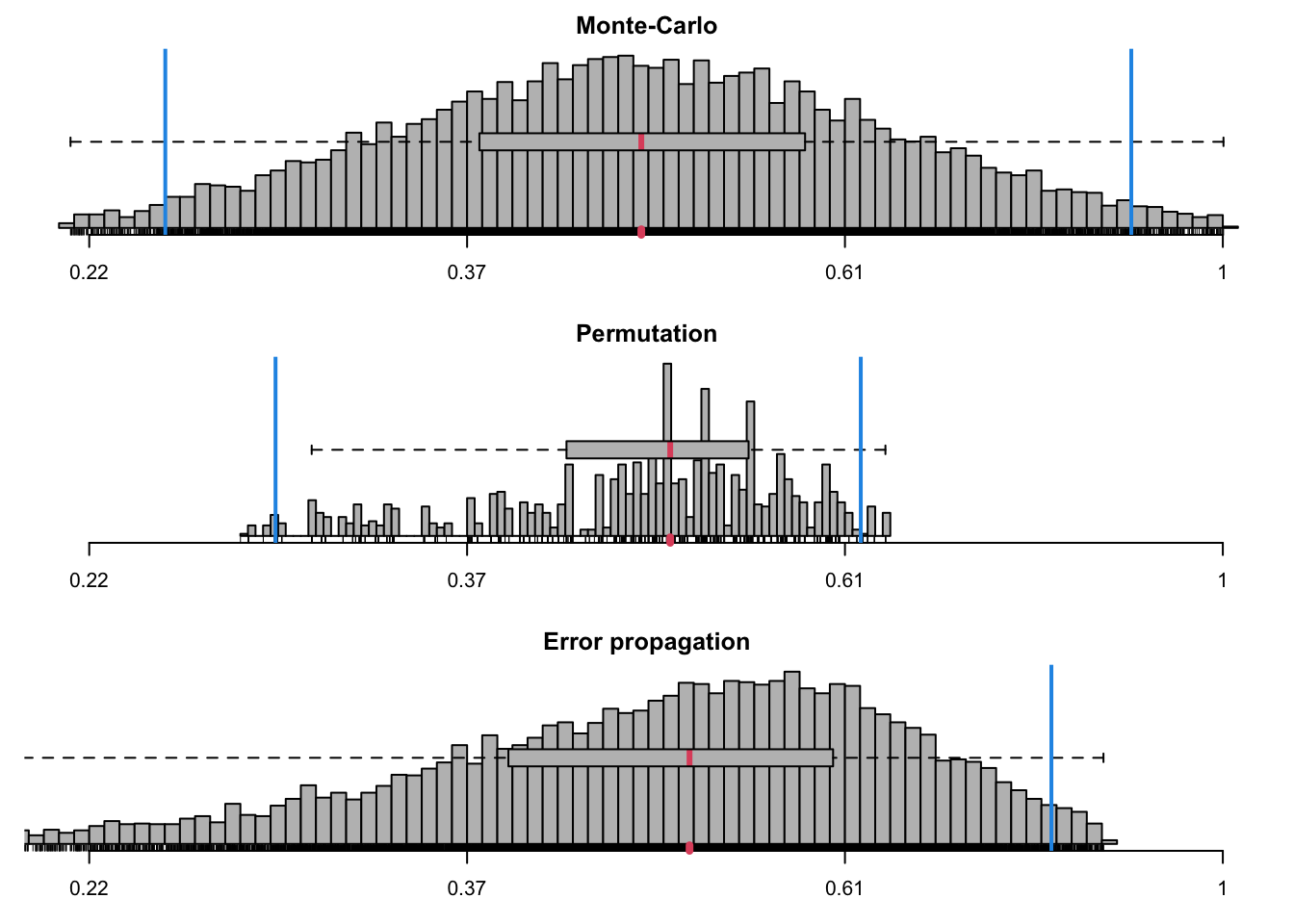
cdh_ratios$summary## Sim Perm Prop
## Mean 0.4903858 0.47236452 0.4896362
## Std.dev. 0.1663977 0.08868237 0.1568446
## Median 0.4632548 0.48132097 NA
## MAD 0.1501247 0.08218529 NA
## Conf.lower 0.2467545 0.28550627 0.1822264
## Conf.upper 0.8859054 0.61935709 0.7970459
## perm > init NA 0.48764045 NA
## perm == init NA 0.51235955 NA
## perm < init NA 0.00000000 NA# make a note of model data was fitted to
cdh_ratios$summary$model <- c("sigmoidal")
# uncomment to save results locally
#write.table(cdh_ratios, file="cdh_cdhUP/qpcR_ratios_cdh.txt", sep="\t", quote=F)- We generate a violin plot of all the permuted values computed during
ratiocalc. This should reflect the boxplot generated by the software.
There are two sets of permuted values. Perm1 results from sampling values based on replicates, while Perm2 results from sampling values based on condition - see propagate documentation for more details.
cdh_points_cp <- na.omit(data.frame(cdh_ratios$data.Perm$resPERM, cdh_ratios$data.Perm$resPERM2))
colnames(cdh_points_cp) <- c("perm1","perm2")
cdh_points_cp$model <- c("sigmoidal")plot <- ggplot(cdh_points_cp, aes(x=model, y=perm1, fill=model)) +
geom_violin(trim=FALSE) +
geom_boxplot(width=0.05, fill="white") + # median and quartiles
labs(title="Distribution of permuted ratios (cdh7a_guides/scr_guides)", y = "Ratio (cdh7a, normalised to gapdh)")
plot + scale_fill_brewer(palette="Dark2") + theme_minimal()
If Perm2 values are desired, use y=perm2.
data_cdhUP (sgRNAs targeting Group Upstream enhancers only)
Essentially a repeat of the above.
- Set (non) random seed for reproducibility
- Reorganise the data in the exact format required for qpcR package
- Runs
pcrbatchfunction to fit sigmoidal model and calculate qPCR efficiency by the ‘window-of-linearity’ method - View if any Runs are tagged
*NAME*/**NAME**due to unsuccessful model fitting/lack of sigmoidal structure
set.seed(584)
data_cdhUP <- tidyr::spread(data_cdhUP, Run, Rn)
res_cdhUP <- pcrbatch(data_cdhUP, cyc = 1, fluo = NULL,
methods = c("sigfit", "sliwin"),
plot = TRUE,
verbose = FALSE)## Calculating delta of first/second derivative maxima...
## .........10.........20.........30.........40.........50
## .........60
##
## [1] "modlist" "pcrfit"
## Analyzing cdhUP^cdh7a*A1_cdh1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdhUP^cdh7a*A10_cdh2-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdhUP^cdh7a*A11_cdh2-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdhUP^cdh7a*A12_cdh2-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdhUP^cdh7a*A2_cdh1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdhUP^cdh7a*A3_cdh1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdhUP^cdh7a*A4_cdh1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdhUP^cdh7a*A5_cdh1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdhUP^cdh7a*A6_cdh1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdhUP^cdh7a*A7_cdh2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdhUP^cdh7a*A8_cdh2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdhUP^cdh7a*A9_cdh2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdhUP^gapdh*C1_cdh1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdhUP^gapdh*C10_cdh2-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdhUP^gapdh*C11_cdh2-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdhUP^gapdh*C12_cdh2-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdhUP^gapdh*C2_cdh1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdhUP^gapdh*C3_cdh1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdhUP^gapdh*C4_cdh1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdhUP^gapdh*C5_cdh1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdhUP^gapdh*C6_cdh1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdhUP^gapdh*C7_cdh2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdhUP^gapdh*C8_cdh2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing cdhUP^gapdh*C9_cdh2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*A10_scr1_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*A10_scr2_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*A11_scr1_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*A11_scr2_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*A12_scr1_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*A12_scr2_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*A7_scr1_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*A7_scr2_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*A8_scr1_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*A8_scr2_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*A9_scr1_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*A9_scr2_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*B1_scr1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*B2_scr1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*B3_scr1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*B4_scr1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*B5_scr1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^cdh7a*B6_scr1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B1_scr1_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B10_scr2_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B11_scr2_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B12_scr2_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B2_scr1_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B3_scr1_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B4_scr1_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B5_scr1_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B6_scr1_2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B7_scr2_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B8_scr2_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B9_scr2_1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*D1_scr1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*D2_scr1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*D3_scr1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*D4_scr1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*D5_scr1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*D6_scr1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...colnames(res_cdhUP)## [1] "Vars" "cdhUP^cdh7a*A1_cdh1-1" "cdhUP^cdh7a*A10_cdh2-2"
## [4] "cdhUP^cdh7a*A11_cdh2-2" "cdhUP^cdh7a*A12_cdh2-2" "cdhUP^cdh7a*A2_cdh1-1"
## [7] "cdhUP^cdh7a*A3_cdh1-1" "cdhUP^cdh7a*A4_cdh1-2" "cdhUP^cdh7a*A5_cdh1-2"
## [10] "cdhUP^cdh7a*A6_cdh1-2" "cdhUP^cdh7a*A7_cdh2-1" "cdhUP^cdh7a*A8_cdh2-1"
## [13] "cdhUP^cdh7a*A9_cdh2-1" "cdhUP^gapdh*C1_cdh1-1" "cdhUP^gapdh*C10_cdh2-2"
## [16] "cdhUP^gapdh*C11_cdh2-2" "cdhUP^gapdh*C12_cdh2-2" "cdhUP^gapdh*C2_cdh1-1"
## [19] "cdhUP^gapdh*C3_cdh1-1" "cdhUP^gapdh*C4_cdh1-2" "cdhUP^gapdh*C5_cdh1-2"
## [22] "cdhUP^gapdh*C6_cdh1-2" "cdhUP^gapdh*C7_cdh2-1" "cdhUP^gapdh*C8_cdh2-1"
## [25] "cdhUP^gapdh*C9_cdh2-1" "scr^cdh7a*A10_scr1_2" "scr^cdh7a*A10_scr2_2"
## [28] "scr^cdh7a*A11_scr1_2" "scr^cdh7a*A11_scr2_2" "scr^cdh7a*A12_scr1_2"
## [31] "scr^cdh7a*A12_scr2_2" "scr^cdh7a*A7_scr1_1" "scr^cdh7a*A7_scr2_1"
## [34] "scr^cdh7a*A8_scr1_1" "scr^cdh7a*A8_scr2_1" "scr^cdh7a*A9_scr1_1"
## [37] "scr^cdh7a*A9_scr2_1" "scr^cdh7a*B1_scr1-1" "scr^cdh7a*B2_scr1-1"
## [40] "scr^cdh7a*B3_scr1-1" "scr^cdh7a*B4_scr1-2" "scr^cdh7a*B5_scr1-2"
## [43] "scr^cdh7a*B6_scr1-2" "scr^gapdh*B1_scr1_1" "scr^gapdh*B10_scr2_2"
## [46] "scr^gapdh*B11_scr2_2" "scr^gapdh*B12_scr2_2" "scr^gapdh*B2_scr1_1"
## [49] "scr^gapdh*B3_scr1_1" "scr^gapdh*B4_scr1_2" "scr^gapdh*B5_scr1_2"
## [52] "scr^gapdh*B6_scr1_2" "scr^gapdh*B7_scr2_1" "scr^gapdh*B8_scr2_1"
## [55] "scr^gapdh*B9_scr2_1" "scr^gapdh*D1_scr1-1" "scr^gapdh*D2_scr1-1"
## [58] "scr^gapdh*D3_scr1-1" "scr^gapdh*D4_scr1-2" "scr^gapdh*D5_scr1-2"
## [61] "scr^gapdh*D6_scr1-2"No runs tagged, so proceed with calculating ratios between experimental conditions.
- We assign each Run into their respective group, in the order shown with
colnames(res_cdhUP).
- “gs” = gene-of-interest, sample (experimental)
- “rs” = reference gene, sample (experimental)
- “gc” = gene-of-interest, control (scrambled)
- “rc” = reference gene, control (scrambled)
group_cdhUP <- rep(c("gs","rs","gc","rc"), times=c(12,12,18,18))- Finally, we compute the ratios between the two conditions (treatment/control) - see
ratiocalcdocumentation for more details. We are interested in the Permutation results (not Monte Carlo or Error Propagation) - seepropagatedocumentation for more details.
cdhUP_ratios <- ratiocalc(res_cdhUP, group = group_cdhUP, plot = TRUE,
which.eff = "sli", type.eff="mean.single", which.cp="cpD2")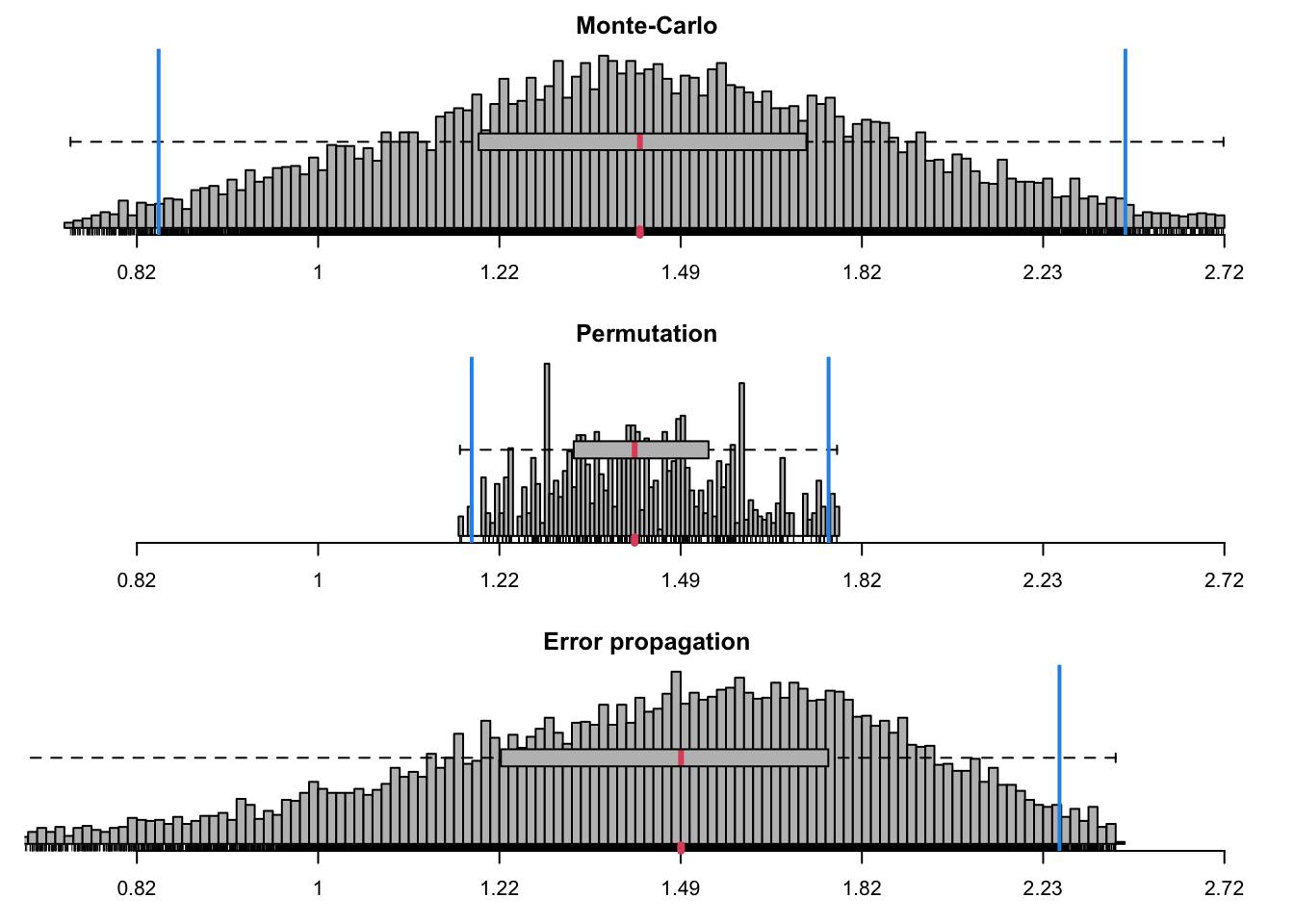
cdhUP_ratios$summary## Sim Perm Prop
## Mean 1.4834712 1.4368529 1.4823906
## Std.dev. 0.4160095 0.1517290 0.3998299
## Median 1.4262932 1.4180290 NA
## MAD 0.3850608 0.1589046 NA
## Conf.lower 0.8385856 1.1846037 0.6987384
## Conf.upper 2.4369906 1.7563898 2.2660428
## perm > init NA 0.0000000 NA
## perm == init NA 0.5123596 NA
## perm < init NA 0.4876404 NA# make a note of model data was fitted to
cdhUP_ratios$summary$model <- c("sigmoidal")
# uncomment to save results locally
#write.table(cdh_ratios, file="cdh_cdhUP/qpcR_ratios_cdh.txt", sep="\t", quote=F)- We generate a violin plot of all the permuted values computed during
ratiocalc. This should reflect the boxplot generated by the software.
There are two sets of permuted values. Perm1 results from sampling values based on replicates, while Perm2 results from sampling values based on condition - see propagate documentation for more details.
cdhUP_points_cp <- na.omit(data.frame(cdhUP_ratios$data.Perm$resPERM, cdhUP_ratios$data.Perm$resPERM2))
colnames(cdhUP_points_cp) <- c("perm1","perm2")
cdhUP_points_cp$model <- c("sigmoidal")plotUP <- ggplot(cdhUP_points_cp, aes(x=model, y=perm1, fill=model)) +
geom_violin(trim=FALSE) +
geom_boxplot(width=0.05, fill="white") + # median and quartiles
labs(title="Distribution of permuted ratios (cdh7a_guides/scr_guides)", y = "Ratio (cdh7a, normalised to gapdh)")
plotUP + scale_fill_brewer(palette="Dark2") + theme_minimal()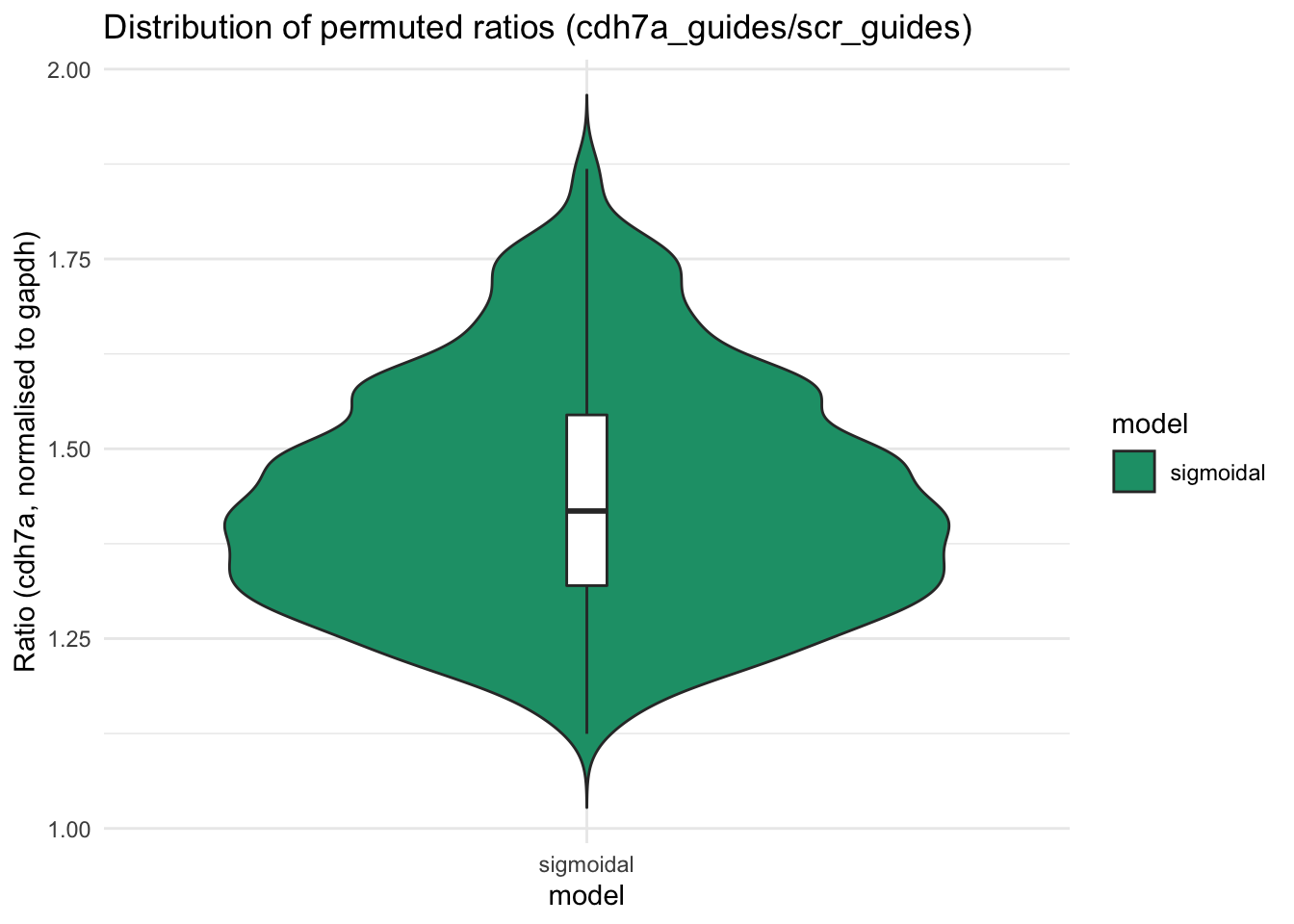
If Perm2 values are desired, use y=perm2.
pdgfra enhancers
As above, but here, my data is split across two dataframes/plates.
data5 <- data.frame(read.table("./data5.txt", header=TRUE, sep="\t"))
data6 <- data.frame(read.table("./data6.txt", header=TRUE, sep="\t"))
head(data5, 10)## Cycles Run Rn
## 1 1 pdgfra*A1_pdg1-1 1.6647
## 2 2 pdgfra*A1_pdg1-1 1.6507
## 3 3 pdgfra*A1_pdg1-1 1.6416
## 4 4 pdgfra*A1_pdg1-1 1.6387
## 5 5 pdgfra*A1_pdg1-1 1.6357
## 6 6 pdgfra*A1_pdg1-1 1.6381
## 7 7 pdgfra*A1_pdg1-1 1.6374
## 8 8 pdgfra*A1_pdg1-1 1.6381
## 9 9 pdgfra*A1_pdg1-1 1.6342
## 10 10 pdgfra*A1_pdg1-1 1.6405Add Group column based on experimental condition.
- pdg = upstream sgRNAs
- scr = scrambled sgRNAs
data5$Group <- rep(c("pdg","scr","pdg","scr"), times=c(240,240,240,240))
data6$Group <- rep(c("pdg","scr","pdg","scr"), times=c(240,240,240,240))
head(data5, 10)## Cycles Run Rn Group
## 1 1 pdgfra*A1_pdg1-1 1.6647 pdg
## 2 2 pdgfra*A1_pdg1-1 1.6507 pdg
## 3 3 pdgfra*A1_pdg1-1 1.6416 pdg
## 4 4 pdgfra*A1_pdg1-1 1.6387 pdg
## 5 5 pdgfra*A1_pdg1-1 1.6357 pdg
## 6 6 pdgfra*A1_pdg1-1 1.6381 pdg
## 7 7 pdgfra*A1_pdg1-1 1.6374 pdg
## 8 8 pdgfra*A1_pdg1-1 1.6381 pdg
## 9 9 pdgfra*A1_pdg1-1 1.6342 pdg
## 10 10 pdgfra*A1_pdg1-1 1.6405 pdgFinal tidying up. Prefix Group (experimental condition) to existing Run names, check all is in order, then rename columns back to Cycles, Run, Rn.
data5 <- data.frame(data5$Cycles, (paste(data5$Group,data5$Run,sep="^")), data5$Rn)
data6 <- data.frame(data6$Cycles, (paste(data6$Group,data6$Run,sep="^")), data6$Rn)
head(data5, 10)## data5.Cycles X.paste.data5.Group..data5.Run..sep........ data5.Rn
## 1 1 pdg^pdgfra*A1_pdg1-1 1.6647
## 2 2 pdg^pdgfra*A1_pdg1-1 1.6507
## 3 3 pdg^pdgfra*A1_pdg1-1 1.6416
## 4 4 pdg^pdgfra*A1_pdg1-1 1.6387
## 5 5 pdg^pdgfra*A1_pdg1-1 1.6357
## 6 6 pdg^pdgfra*A1_pdg1-1 1.6381
## 7 7 pdg^pdgfra*A1_pdg1-1 1.6374
## 8 8 pdg^pdgfra*A1_pdg1-1 1.6381
## 9 9 pdg^pdgfra*A1_pdg1-1 1.6342
## 10 10 pdg^pdgfra*A1_pdg1-1 1.6405colnames(data5) <- c("Cycles", "Run", "Rn")
colnames(data6) <- c("Cycles", "Run", "Rn")
head(data5, 10)## Cycles Run Rn
## 1 1 pdg^pdgfra*A1_pdg1-1 1.6647
## 2 2 pdg^pdgfra*A1_pdg1-1 1.6507
## 3 3 pdg^pdgfra*A1_pdg1-1 1.6416
## 4 4 pdg^pdgfra*A1_pdg1-1 1.6387
## 5 5 pdg^pdgfra*A1_pdg1-1 1.6357
## 6 6 pdg^pdgfra*A1_pdg1-1 1.6381
## 7 7 pdg^pdgfra*A1_pdg1-1 1.6374
## 8 8 pdg^pdgfra*A1_pdg1-1 1.6381
## 9 9 pdg^pdgfra*A1_pdg1-1 1.6342
## 10 10 pdg^pdgfra*A1_pdg1-1 1.6405qpcR analysis
- Set (non) random seed for reproducibility
- Reorganise the data in the exact format required for qpcR package
- Run
pcrbatchfunction to fit sigmoidal model and calculate qPCR efficiency by the ‘window-of-linearity’ method - View if any Runs are tagged
*NAME*/**NAME**due to unsuccessful model fitting/lack of sigmoidal structure
set.seed(584)
data_pdg <- data.frame(rbind(data5,data6))
data_pdg <- tidyr::spread(data_pdg, Run, Rn)
res_pdg <- pcrbatch(data_pdg, cyc = 1, fluo = NULL,
methods = c("sigfit", "sliwin"),
plot = TRUE,
verbose = FALSE)## Calculating delta of first/second derivative maxima...
## .........10.........20.........30.........40........
## Found univariate outlier for pdg^gapdh*B3_pdg2-1 pdg^gapdh*B4_pdg2-2 pdg^gapdh*B5_pdg2-2 pdg^gapdh*B6_pdg2-2 pdg^pdgfra*A4_pdg2-2
## Tagging name of pdg^gapdh*B3_pdg2-1 pdg^gapdh*B4_pdg2-2 pdg^gapdh*B5_pdg2-2 pdg^gapdh*B6_pdg2-2 pdg^pdgfra*A4_pdg2-2 ...
##
## [1] "modlist" "pcrfit"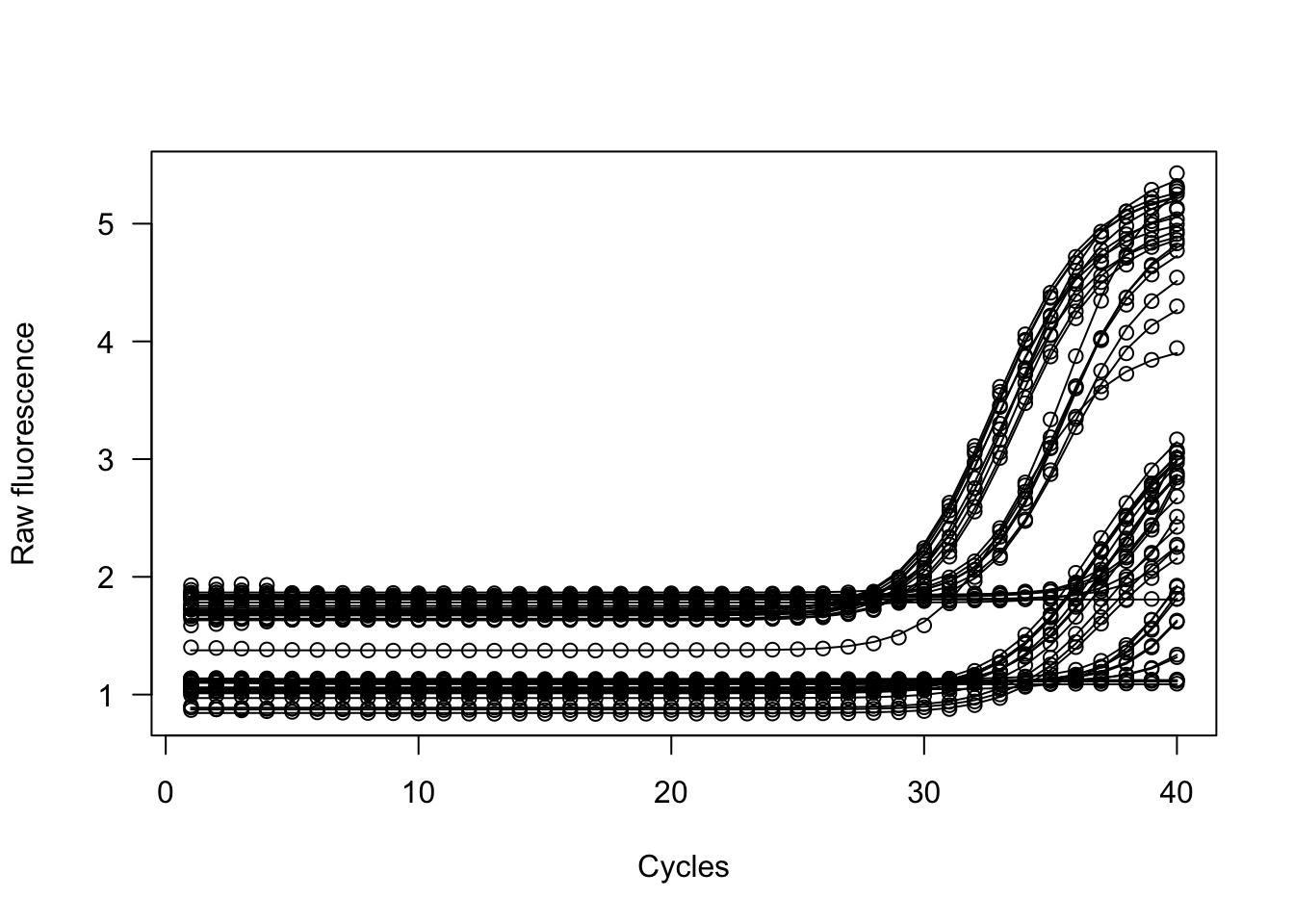
## Analyzing pdg^gapdh*B1_pdg2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^gapdh*B2_pdg2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing **pdg^gapdh*B3_pdg2-1** ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing **pdg^gapdh*B4_pdg2-2** ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing **pdg^gapdh*B5_pdg2-2** ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing **pdg^gapdh*B6_pdg2-2** ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^gapdh*D1_pdg1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^gapdh*D2_pdg1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^gapdh*D3_pdg1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^gapdh*D4_pdg1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^gapdh*D5_pdg1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^gapdh*D6_pdg1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^pdgfra*A1_pdg1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^pdgfra*A1_pdg2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^pdgfra*A2_pdg1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^pdgfra*A2_pdg2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^pdgfra*A3_pdg1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^pdgfra*A3_pdg2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^pdgfra*A4_pdg1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing **pdg^pdgfra*A4_pdg2-2** ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^pdgfra*A5_pdg1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^pdgfra*A5_pdg2-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^pdgfra*A6_pdg1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^pdgfra*A6_pdg2-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B10_scr2-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B11_scr2-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B12_scr2-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B7_scr2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B8_scr2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B9_scr2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*E1_scr1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*E2_scr1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*E3_scr1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*E4_scr1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*E5_scr1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*E6_scr1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^pdgfra*A10_scr2-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^pdgfra*A11_scr2-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^pdgfra*A12_scr2-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^pdgfra*A7_scr2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^pdgfra*A8_scr2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^pdgfra*A9_scr2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^pdgfra*B1_scr1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^pdgfra*B2_scr1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^pdgfra*B3_scr1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^pdgfra*B4_scr1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^pdgfra*B5_scr1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^pdgfra*B6_scr1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...colnames(res_pdg)## [1] "Vars" "pdg^gapdh*B1_pdg2-1"
## [3] "pdg^gapdh*B2_pdg2-1" "**pdg^gapdh*B3_pdg2-1**"
## [5] "**pdg^gapdh*B4_pdg2-2**" "**pdg^gapdh*B5_pdg2-2**"
## [7] "**pdg^gapdh*B6_pdg2-2**" "pdg^gapdh*D1_pdg1-1"
## [9] "pdg^gapdh*D2_pdg1-1" "pdg^gapdh*D3_pdg1-1"
## [11] "pdg^gapdh*D4_pdg1-2" "pdg^gapdh*D5_pdg1-2"
## [13] "pdg^gapdh*D6_pdg1-2" "pdg^pdgfra*A1_pdg1-1"
## [15] "pdg^pdgfra*A1_pdg2-1" "pdg^pdgfra*A2_pdg1-1"
## [17] "pdg^pdgfra*A2_pdg2-1" "pdg^pdgfra*A3_pdg1-1"
## [19] "pdg^pdgfra*A3_pdg2-1" "pdg^pdgfra*A4_pdg1-2"
## [21] "**pdg^pdgfra*A4_pdg2-2**" "pdg^pdgfra*A5_pdg1-2"
## [23] "pdg^pdgfra*A5_pdg2-2" "pdg^pdgfra*A6_pdg1-2"
## [25] "pdg^pdgfra*A6_pdg2-2" "scr^gapdh*B10_scr2-2"
## [27] "scr^gapdh*B11_scr2-2" "scr^gapdh*B12_scr2-2"
## [29] "scr^gapdh*B7_scr2-1" "scr^gapdh*B8_scr2-1"
## [31] "scr^gapdh*B9_scr2-1" "scr^gapdh*E1_scr1-1"
## [33] "scr^gapdh*E2_scr1-1" "scr^gapdh*E3_scr1-1"
## [35] "scr^gapdh*E4_scr1-2" "scr^gapdh*E5_scr1-2"
## [37] "scr^gapdh*E6_scr1-2" "scr^pdgfra*A10_scr2-2"
## [39] "scr^pdgfra*A11_scr2-2" "scr^pdgfra*A12_scr2-2"
## [41] "scr^pdgfra*A7_scr2-1" "scr^pdgfra*A8_scr2-1"
## [43] "scr^pdgfra*A9_scr2-1" "scr^pdgfra*B1_scr1-1"
## [45] "scr^pdgfra*B2_scr1-1" "scr^pdgfra*B3_scr1-1"
## [47] "scr^pdgfra*B4_scr1-2" "scr^pdgfra*B5_scr1-2"
## [49] "scr^pdgfra*B6_scr1-2"Some runs lack sigmoidal structure (**NAME**) i.e. failed to amplify. Re-run pcrbatch, this time excluding unsuccessful Run(s).
res_pdg <- pcrbatch(data_pdg, cyc = 1, fluo = NULL,
methods = c("sigfit", "sliwin"),
plot = TRUE,
verbose = FALSE,
remove="KOD") # or "fit" for Runs with unsuccessful model fitting)## Calculating delta of first/second derivative maxima...
## .........10.........20.........30.........40........
## Found univariate outlier for pdg^gapdh*B3_pdg2-1 pdg^gapdh*B4_pdg2-2 pdg^gapdh*B5_pdg2-2 pdg^gapdh*B6_pdg2-2 pdg^pdgfra*A4_pdg2-2
## Tagging name of pdg^gapdh*B3_pdg2-1 pdg^gapdh*B4_pdg2-2 pdg^gapdh*B5_pdg2-2 pdg^gapdh*B6_pdg2-2 pdg^pdgfra*A4_pdg2-2 ...
##
## [1] "modlist" "pcrfit"
## Analyzing pdg^gapdh*B1_pdg2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^gapdh*B2_pdg2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^gapdh*D1_pdg1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^gapdh*D2_pdg1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^gapdh*D3_pdg1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^gapdh*D4_pdg1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^gapdh*D5_pdg1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^gapdh*D6_pdg1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^pdgfra*A1_pdg1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^pdgfra*A1_pdg2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^pdgfra*A2_pdg1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^pdgfra*A2_pdg2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^pdgfra*A3_pdg1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^pdgfra*A3_pdg2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^pdgfra*A4_pdg1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^pdgfra*A5_pdg1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^pdgfra*A5_pdg2-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^pdgfra*A6_pdg1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing pdg^pdgfra*A6_pdg2-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B10_scr2-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B11_scr2-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B12_scr2-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B7_scr2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B8_scr2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*B9_scr2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*E1_scr1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*E2_scr1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*E3_scr1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*E4_scr1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*E5_scr1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^gapdh*E6_scr1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^pdgfra*A10_scr2-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^pdgfra*A11_scr2-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^pdgfra*A12_scr2-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^pdgfra*A7_scr2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^pdgfra*A8_scr2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^pdgfra*A9_scr2-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^pdgfra*B1_scr1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^pdgfra*B2_scr1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^pdgfra*B3_scr1-1 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^pdgfra*B4_scr1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^pdgfra*B5_scr1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...
##
## Analyzing scr^pdgfra*B6_scr1-2 ...
## Calculating 'eff' and 'ct' from sigmoidal model...
## Using window-of-linearity...colnames(res_pdg)## [1] "Vars" "pdg^gapdh*B1_pdg2-1" "pdg^gapdh*B2_pdg2-1"
## [4] "pdg^gapdh*D1_pdg1-1" "pdg^gapdh*D2_pdg1-1" "pdg^gapdh*D3_pdg1-1"
## [7] "pdg^gapdh*D4_pdg1-2" "pdg^gapdh*D5_pdg1-2" "pdg^gapdh*D6_pdg1-2"
## [10] "pdg^pdgfra*A1_pdg1-1" "pdg^pdgfra*A1_pdg2-1" "pdg^pdgfra*A2_pdg1-1"
## [13] "pdg^pdgfra*A2_pdg2-1" "pdg^pdgfra*A3_pdg1-1" "pdg^pdgfra*A3_pdg2-1"
## [16] "pdg^pdgfra*A4_pdg1-2" "pdg^pdgfra*A5_pdg1-2" "pdg^pdgfra*A5_pdg2-2"
## [19] "pdg^pdgfra*A6_pdg1-2" "pdg^pdgfra*A6_pdg2-2" "scr^gapdh*B10_scr2-2"
## [22] "scr^gapdh*B11_scr2-2" "scr^gapdh*B12_scr2-2" "scr^gapdh*B7_scr2-1"
## [25] "scr^gapdh*B8_scr2-1" "scr^gapdh*B9_scr2-1" "scr^gapdh*E1_scr1-1"
## [28] "scr^gapdh*E2_scr1-1" "scr^gapdh*E3_scr1-1" "scr^gapdh*E4_scr1-2"
## [31] "scr^gapdh*E5_scr1-2" "scr^gapdh*E6_scr1-2" "scr^pdgfra*A10_scr2-2"
## [34] "scr^pdgfra*A11_scr2-2" "scr^pdgfra*A12_scr2-2" "scr^pdgfra*A7_scr2-1"
## [37] "scr^pdgfra*A8_scr2-1" "scr^pdgfra*A9_scr2-1" "scr^pdgfra*B1_scr1-1"
## [40] "scr^pdgfra*B2_scr1-1" "scr^pdgfra*B3_scr1-1" "scr^pdgfra*B4_scr1-2"
## [43] "scr^pdgfra*B5_scr1-2" "scr^pdgfra*B6_scr1-2"- Proceed with calculating ratios between experimental conditions. We assign each Run into their respective group, in the order shown with
colnames(res_pdg).
- “gs” = gene-of-interest, sample (experimental)
- “rs” = reference gene, sample (experimental)
- “gc” = gene-of-interest, control (scrambled)
- “rc” = reference gene, control (scrambled)
group_pdg <- rep(c("rs","gs","rc","gc"), times=c(8,11,12,12))- Finally, we compute the ratios between the two conditions (treatment/control) - see
ratiocalcdocumentation for more details. We are interested in the Permutation results (not Monte Carlo or Error Propagation) - seepropagatedocumentation for more details.
pdg_ratios <- ratiocalc(res_pdg, group = group_pdg, plot = TRUE,
which.eff = "sli", type.eff="mean.single", which.cp="cpD2")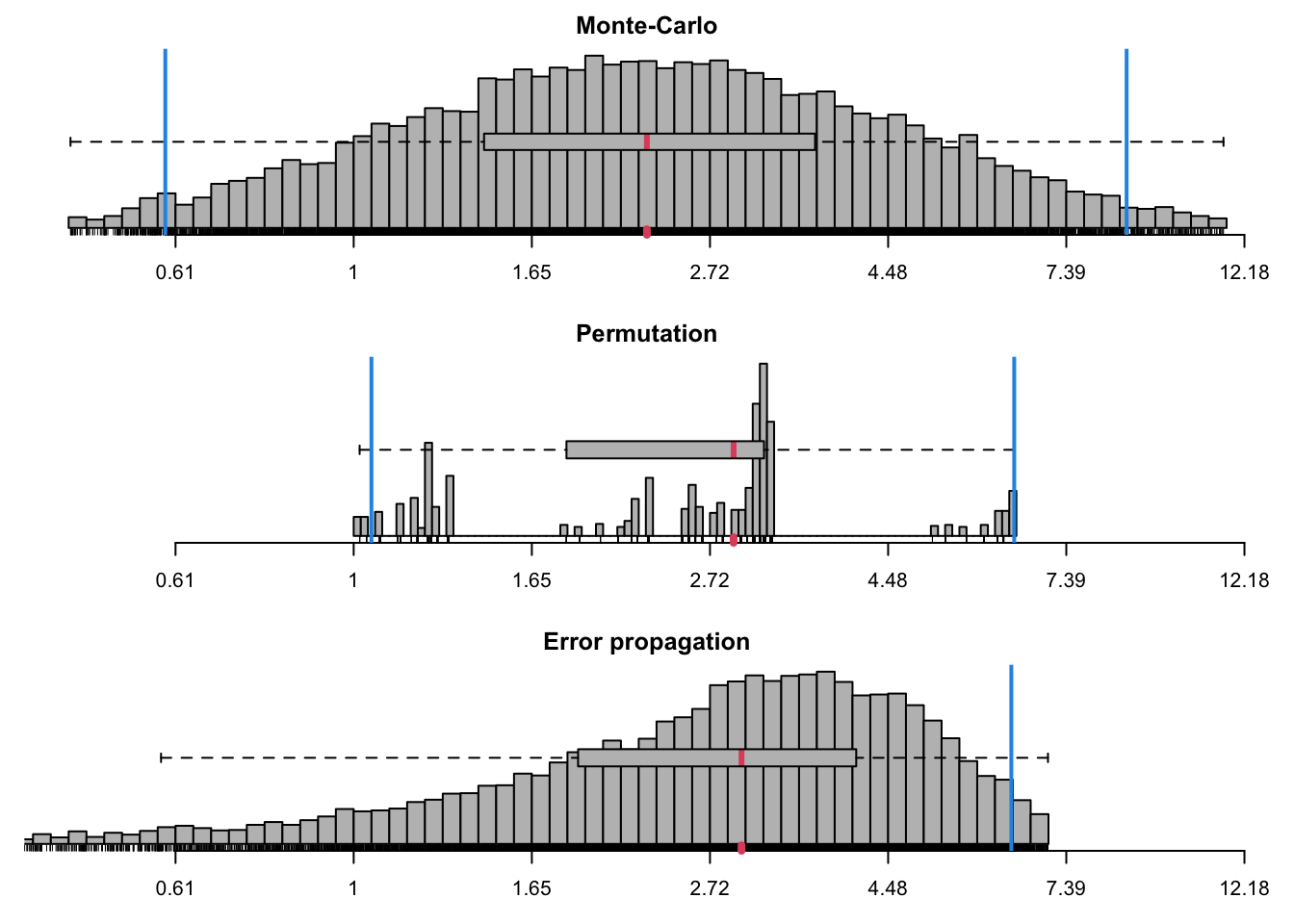
pdg_ratios$summary## Sim Perm Prop
## Mean 2.9192773 2.80560905 2.841954
## Std.dev. 2.3748316 1.42671692 1.781097
## Median 2.2771163 2.90452071 NA
## MAD 1.5104917 0.57644863 NA
## Conf.lower 0.5893558 1.05107432 -0.648931
## Conf.upper 8.7523456 6.38423735 6.332840
## perm > init NA 0.01055011 NA
## perm == init NA 0.51243406 NA
## perm < init NA 0.47701583 NA# make a note of model data was fitted to
pdg_ratios$summary$model <- c("sigmoidal")
# uncomment to save results locally
#write.table(pdg_ratios, file="./qpcR_ratios_pdg.txt", sep="\t", quote=F)- We generate a violin plot of all the permuted values computed during
ratiocalc. This should reflect the boxplot generated by the software.
There are two sets of permuted values. Perm1 results from sampling values based on replicates, while Perm2 results from sampling values based on condition - see propagate documentation for more details.
pdg_points_cp <- na.omit(data.frame(pdg_ratios$data.Perm$resPERM, pdg_ratios$data.Perm$resPERM2))
colnames(pdg_points_cp) <- c("perm1","perm2")
pdg_points_cp$model <- c("sigmoidal")plot_pdg <- ggplot(pdg_points_cp, aes(x=model, y=perm1, fill=model)) +
geom_violin(trim=FALSE) +
geom_boxplot(width=0.05, fill="white") + # median and quartiles
labs(title="Distribution of permuted ratios (pdgfra_guides/scr_guides)", y = "Ratio (pdgfra, normalised to gapdh)")
plot_pdg + scale_fill_brewer(palette="Dark2") + theme_minimal()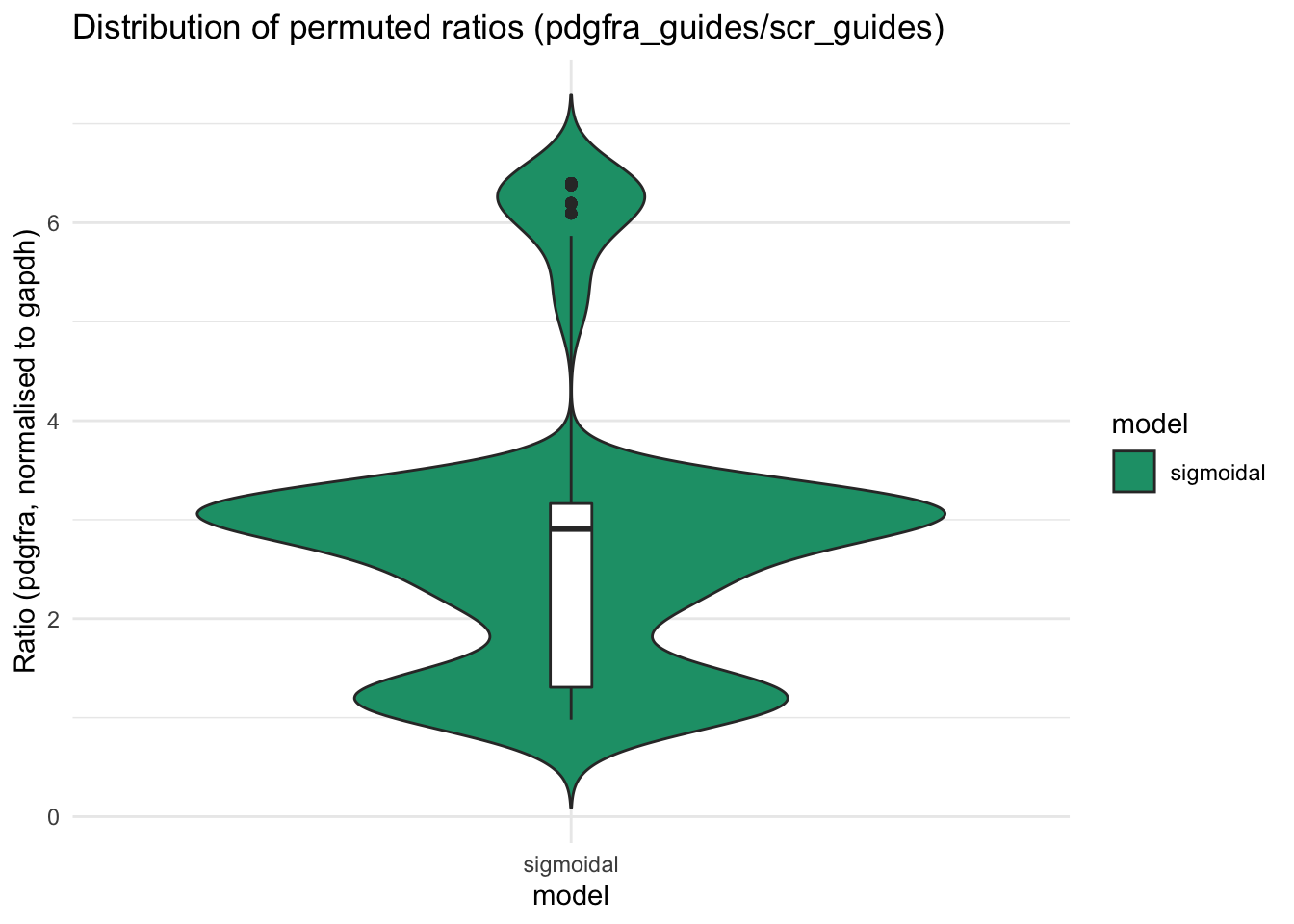
If Perm2 values are desired, use y=perm2.
sessionInfo()## R version 4.2.1 (2022-06-23)
## Platform: x86_64-apple-darwin17.0 (64-bit)
## Running under: macOS Mojave 10.14.6
##
## Matrix products: default
## BLAS: /Library/Frameworks/R.framework/Versions/4.2/Resources/lib/libRblas.0.dylib
## LAPACK: /Library/Frameworks/R.framework/Versions/4.2/Resources/lib/libRlapack.dylib
##
## locale:
## [1] en_GB.UTF-8/en_GB.UTF-8/en_GB.UTF-8/C/en_GB.UTF-8/en_GB.UTF-8
##
## attached base packages:
## [1] stats graphics grDevices utils datasets methods base
##
## other attached packages:
## [1] RColorBrewer_1.1-3 qpcR_1.4-1 Matrix_1.5-1 robustbase_0.95-0
## [5] rgl_0.110.2 minpack.lm_1.2-2 MASS_7.3-58.1 rbioapi_0.7.7
## [9] biomaRt_2.52.0 forcats_0.5.2 stringr_1.4.1 dplyr_1.0.10
## [13] purrr_0.3.5 readr_2.1.3 tidyr_1.2.1 tibble_3.1.8
## [17] ggplot2_3.3.6 tidyverse_1.3.2 sleuth_0.30.0
##
## loaded via a namespace (and not attached):
## [1] googledrive_2.0.0 colorspace_2.0-3 ellipsis_0.3.2
## [4] XVector_0.36.0 base64enc_0.1-3 fs_1.5.2
## [7] rstudioapi_0.14 farver_2.1.1 bit64_4.0.5
## [10] AnnotationDbi_1.58.0 fansi_1.0.3 lubridate_1.8.0
## [13] xml2_1.3.3 cachem_1.0.6 knitr_1.40
## [16] jsonlite_1.8.3 broom_1.0.1 dbplyr_2.2.1
## [19] png_0.1-7 pheatmap_1.0.12 compiler_4.2.1
## [22] httr_1.4.4 backports_1.4.1 assertthat_0.2.1
## [25] fastmap_1.1.0 lazyeval_0.2.2 gargle_1.2.1
## [28] cli_3.4.1 htmltools_0.5.3 prettyunits_1.1.1
## [31] tools_4.2.1 gtable_0.3.1 glue_1.6.2
## [34] GenomeInfoDbData_1.2.8 reshape2_1.4.4 rappdirs_0.3.3
## [37] Rcpp_1.0.9 Biobase_2.56.0 cellranger_1.1.0
## [40] jquerylib_0.1.4 vctrs_0.5.0 Biostrings_2.64.1
## [43] rhdf5filters_1.8.0 xfun_0.34 rvest_1.0.3
## [46] lifecycle_1.0.3 XML_3.99-0.11 googlesheets4_1.0.1
## [49] DEoptimR_1.0-11 zlibbioc_1.42.0 scales_1.2.1
## [52] hms_1.1.2 parallel_4.2.1 rhdf5_2.40.0
## [55] yaml_2.3.6 curl_4.3.3 memoise_2.0.1
## [58] gridExtra_2.3 sass_0.4.2 stringi_1.7.8
## [61] RSQLite_2.2.18 highr_0.9 S4Vectors_0.34.0
## [64] BiocGenerics_0.42.0 filelock_1.0.2 GenomeInfoDb_1.32.4
## [67] rlang_1.0.6 pkgconfig_2.0.3 bitops_1.0-7
## [70] matrixStats_0.62.0 lattice_0.20-45 evaluate_0.17
## [73] Rhdf5lib_1.18.2 htmlwidgets_1.5.4 labeling_0.4.2
## [76] bit_4.0.4 tidyselect_1.2.0 plyr_1.8.7
## [79] magrittr_2.0.3 R6_2.5.1 IRanges_2.30.1
## [82] generics_0.1.3 DBI_1.1.3 pillar_1.8.1
## [85] haven_2.5.1 withr_2.5.0 KEGGREST_1.36.3
## [88] RCurl_1.98-1.9 modelr_0.1.9 crayon_1.5.2
## [91] utf8_1.2.2 BiocFileCache_2.4.0 tzdb_0.3.0
## [94] rmarkdown_2.17 progress_1.2.2 grid_4.2.1
## [97] readxl_1.4.1 data.table_1.14.4 blob_1.2.3
## [100] reprex_2.0.2 digest_0.6.30 stats4_4.2.1
## [103] munsell_0.5.0 bslib_0.4.0References
- qpcR download
- qpcR documentation
- qpcR website
- Christian Ritz, Andrej-Nikolai Spiess, qpcR: an R package for sigmoidal model selection in quantitative real-time polymerase chain reaction analysis, Bioinformatics, Volume 24, Issue 13, 1 July 2008, Pages 1549–1551, https://doi.org/10.1093/bioinformatics/btn227